评估博彩实力：贝叶斯方法与频率派方法

博彩玩家如何评估自己的实力水平？

贝叶斯方法与频率派方法存在哪些区别？

随机度和预期实力概率如何？

从最基本的层面上讲，

我此前曾对如何运用频率派方法（t 检验）评估投注历史质量进行过研究。本文将对两种方法进行一番对比。

• 阅读：如何检验情报商记录的可信度

置信度

在概率论中，贝叶斯定理描述了在某事件发生的情况下另一事件发生的可能性。例如，假设我认为自己有 50% 的概率成为能够获利的高水平博彩玩家。那么，如果我下次投注获利，我对上述命题的置信度会受到怎样的影响？换句话说，投注获利这一证据如何改变我成为高水平博彩玩家的概率？

• 成为赢利的博彩玩家：靠运气还是实力

贝叶斯定理认为，概率是对某一命题或假设的“置信度”，并以数学方式形成了证据已知前的先验置信度（先验概率）与说明证据之后的置信度（ 后验概率）之间的关系。其公式如下：

{equation} – P(A|B)= P(A)*P(B|A)/P(B)

在本例中：

P(A) = 我是高水平博彩玩家的先验概率

P(B) = 我投注获利的先验概率

P(B|A) = 基于我是高水平博彩玩家这一条件我投注获利的概率。

P(A|B) = 基于我投注获利这一条件我是高水平博彩玩家的概率。

我们来举例说明一下。假设投资回报率能够持续达到 110% 者方可称为高水平博彩玩家。那么，对于同额投注，意味着每 100 人中有 55 名获利者。因此，基于我是高水平博彩玩家这一条件我投注获利的概率 P(B|A) 为 55%。

对于低水平博彩玩家而言，在公平的同额投注中获利的概率 P(B) 将为 50%。然而，假设我先前认为自己有 50-50 的可能性跻身高水平玩家行列 {P(A) = 50%}，而此等博彩玩家的 P(B) 为 52.5%（即 50% 与 55% 的中间值）。

业内一流让分研究人员的胜率一般能达到 57%。扣除博彩公司的利润之后，投资回报率在 110% 左右。

如果我投注获利，那么将这些数字转换为贝叶斯定理后，得到的后验概率 P(A|B) 将为 52.38%。投注获利后，我认为自己成为高水平博彩玩家的概率比之前更大。

贝叶斯定理支持迭代计算。我在第一笔投注获利并更新自己成为高水平博彩玩家的概率后，现在再次下注。在第一步中计算出的后验概率作为新的先验概率。

我成为高水平博彩玩家的新后验概率现在将以我赢下（或输掉）下笔投注为条件。如果赢，则我成为高水平博彩玩家的概率将再次增加，如果输掉则减少。在本例中，如果我的第二笔投注再次获利，那么我成为高水平博彩玩家的概率将增加到 54.75%。

此过程可无限次重复，更新后的每个条件概率均在 0% 到 100% 之间。我已经运行 1000 次迭代，也就是说投注 1000 次。下图显示了每次投注后所获得的投注历史（蓝线）以及我成为高水平博彩玩家的贝叶斯概率（红线）。

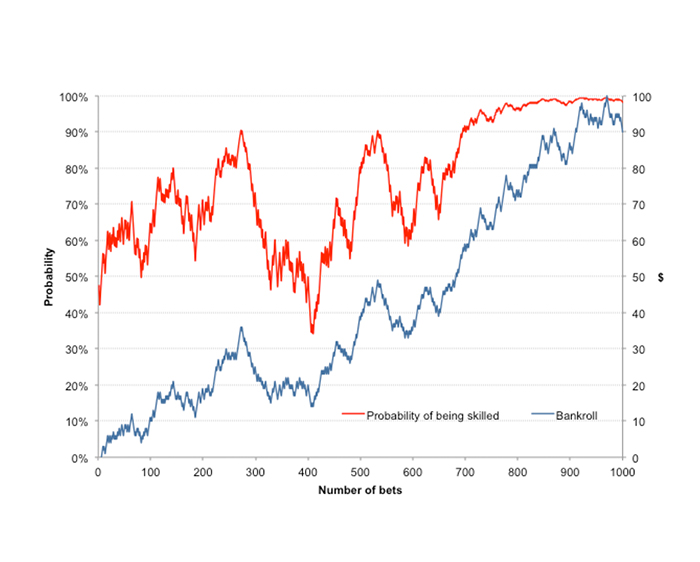
贝叶斯定理对概率的解释存在一个重大问题，那就是要求对某事件或状况有较高的先验认知或置信度。然而，我们在评估自身成为高水平博彩玩家的概率时是否真正具备这一点？在本例中，我选择 50% 完全是随意的，是没有任何依据的一种猜测而已。我们来看一下，如果我现在将初始先验概率改为 1%，将会发生什么？

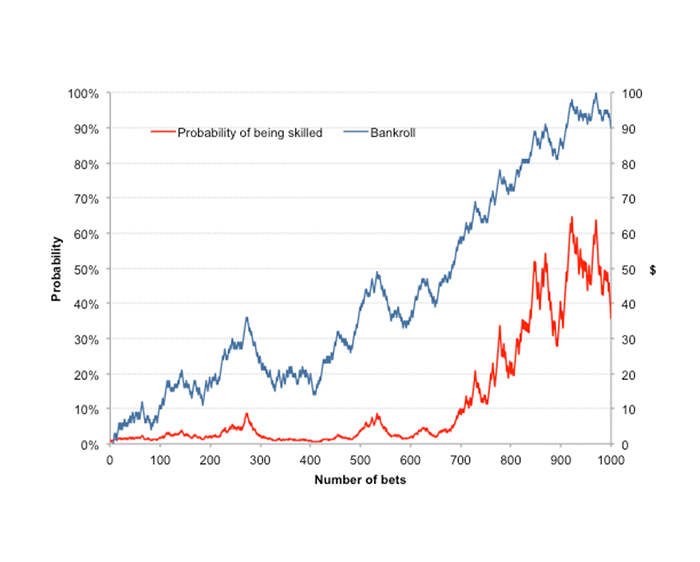
此外，在本上下文中，关于“高水平”的定义也完全是主观性的。可以说，如果某博彩玩家的投资回报率高达 105%，并且能够在超过 10,000 次的投注中达到此值，即认为其属于超高水平博彩玩家。之所以提出 10,000 次，是因为考虑到样本量的重要性。具体内容，请阅读小数定律的相关信息。同样，对于更新后的 P(A) 值，如何为每个迭代步骤定义 P(B) 也并不明确。

在我的贝叶斯模型中，我只是假设这样一种线性关系，如果 P(A) = 0%/20%/40%/60%/80%/100%，那么 P(B) = 50%/51%/52%/53%/54%/55%，但其有效性肯定是有问题的。更重要的一点可能是，由于基准投注胜率达到 52.5% 的博彩玩家本身显然已可以称为高水平玩家（只是比胜率为 55% 的玩家略逊一筹），因此我们这里测量的是实力程度而非实力概率。

尽管如此，该贝叶斯概率演化示意图仍十分有用，可在一定程度上直观测量博彩玩家持续获利能力的可能性（或强度），及其随时间推移可能发生的变化。

随机度

贝叶斯方法主要基于一组固定数据（收益和损失）确定假设条件（我是高水平博彩玩家）的概率，而频率派方法则侧重于给定假设的数据的概率（或频率）。这次的假设条件是固定的，也就是说，关于我能否成为高水平博彩玩家，该条件要么为真（100% 的概率），要么为假（0% 的概率），而假定数据是随机的。

如果关于某人能否成为高水平博彩玩家的初始先验置信度为 1% 的概率，那么经过 1000 次投注后，此值也不过是上升到 20%。

频率派方法通常先设置零假设，即，我不是高水平博彩玩家，我的所有投注结果完全取决于运气。然后该方法尝试在假定零假设为“真”的条件下，通过我们所观察的一些数据的统计信息（在本例中指我的收益和损失记录）计算概率（通常称为“p 值”）。

最后，将该概率与可接受的显著性值（有时称为“α 值”）进行比较，如果 p < α（通常为 5%或 1%），则推翻零假设，选用有效值。

我之前在平博的“博彩资源”中审核的统计值为 t 分数，之所以如此命名，是因为其来源于学生的统计显著性 t 检验。假设投注赔率公平，则可按以下方式近似计算“t 分数”：

其中 n = 投注次数，r = 投资回报率（用小数表示），o = 投注赔率平均值（用小数表示）。通过统计表或在线计算器将“t 分数”转换为“p 值”。在 Excel 中，可使用 TDIST 函数。接下来我们来结合投注历史示例看看此方法的实际应用情况。

下图使用双尾、单样本 t 检验对贝叶斯概率（即，在我成为高水平博彩玩家的先验置信度概率为 50% 的条件下我成为高水平博彩玩家的概率，图中以红线表示）的原始演化时序与频率派“p 值”的演化（即，在假设我毫无实力的条件下我所取得的成果的偶发概率，图中以绿线表示）进行了比较。

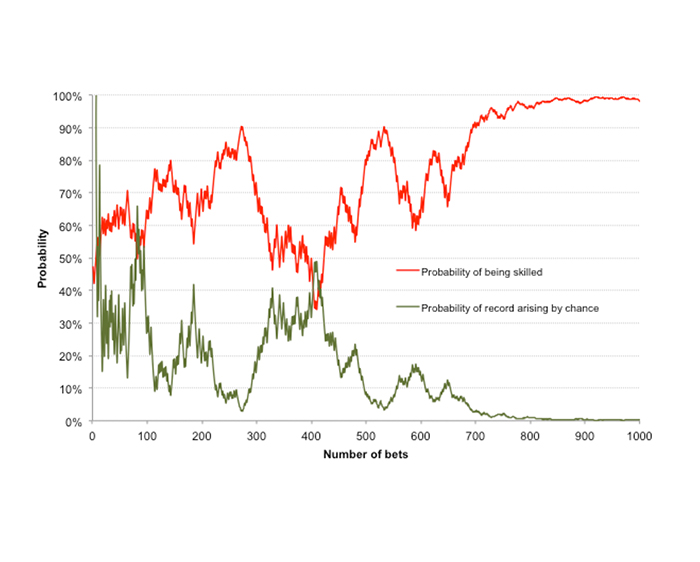
按照一般的定性方式，这两条线截然相反，尽管这很可能是运气好的结果。但我们不应认为“p 值”测量的是低水平概率，因而 1-p 等于高水平概率。

撇开其他作用不谈，贝叶斯和频率派分析能够再次提醒博彩玩家，在博彩中稳定获利需要从长计议。

盈亏历史偶发概率为 5% 并不表示因实力因素发生的概率为 95%。这只是表示，假定投注输赢完全是随机的这一零假设为“真”，那么我们所观察的结果的预期发生率为 5%。

频率派方法的缺点在于其认为真理是绝对的。而贝叶斯方法则间接认为真理具有概率性、临时性以及可证伪性。然而，瑕不掩瑜，频率派假设检验同样为我们提供了一款有用的工具，我们可以用其分析投注历史，并确定这些历史是否有可能在其他非运气因素的作用下发生。

如果贝叶斯模型关于我成为高水平博彩玩家的原始先验置信度为 1%（而非 50%）的概率，那么其与频率派模型的对比情况如何？

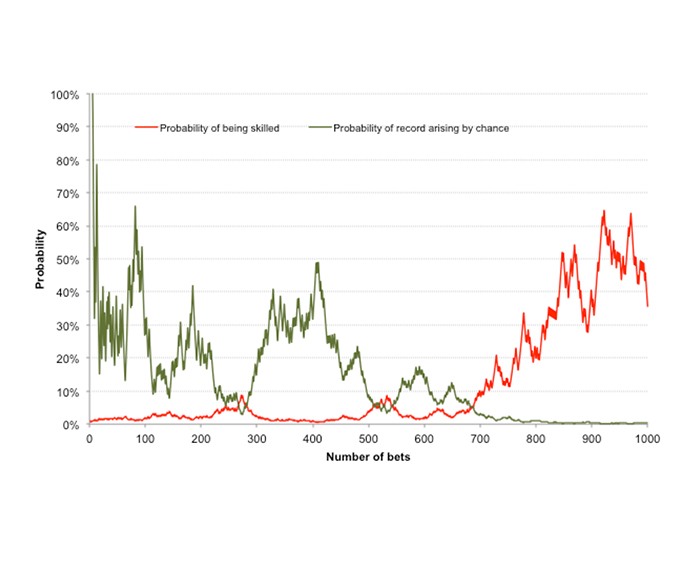
很显然，这次 t 检验结果对我们成为高水平情报商的置信度要高于贝叶斯方法，后者相比之下要保守得多。

这进一步凸显了贝叶斯概率对初始先验置信度的敏感性。对于这种情况，经过近 700 次投注后，t 检验结果可能会认为我们的投注历史的偶发概率只有 3%，而贝叶斯定理则暗示，我们达到长期投资回报率达 110% 的高水平级别只有不到 10% 的可能性。

我本人不喜欢冒险，因而倾向于更加保守的先验实力置信度，除非有充分的理由去质疑，否则我始终会以假定自己实力较差或毫无实力为前提。

预期实力概率

上述分析呈现的只是关于投注时间序列的一个随机示例，其中假设投资回报率为 110%。出于直观呈现的目的，我特意选择了一段投注历史，便于表达所讨论的观点。

如果想详细了解预期情况，即一般情况下的预期，应多次运行模型。熟悉平博“博彩资源”的朋友都知道，我们可以通过蒙特卡罗模拟进行此操作。

• 阅读：使用蒙特卡罗方法分析投注

下面的第一个图显示了在 10 个假设胜率（51% 到 60%，间隔为 1%）的条件下贝叶斯概率（即我成为高水平博彩玩家的概率）演化的 10,000 次蒙特卡罗模拟运行的结果（假定赔率公平，相当于 102% 到 120%，预期值间隔为 2%）。

曲线的形成方式如下：计算 1000 次投注历史期间每次顺序下注后的贝叶斯概率的中间值，因此，此图所反映的信息优于平均值（低值和高值会影响解释的准确性）。

• 了解平均值可能会影响投注预测的原因

假设关于我的实力的初始先验置信度 {p(A)} 为 1%。不出所料，假设胜率（和预期值）越高，对我的能力的置信度达到 100% 概率的速度就越快。（曲线颜色越深，表示假设胜率越高。）

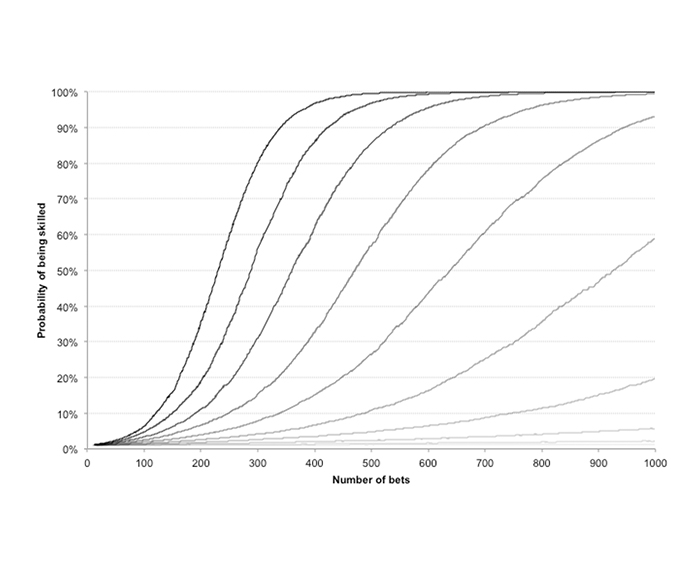
业内一流让分研究人员的胜率一般能达到 57%。扣除博彩公司的利润之后，投资回报率在 110% 左右。此图表明，如果您想跻身上述人群的行列，则需要考察 1000 次投注中的大部分投注信息，才能对自身能力形成深刻、有意义的认知，当然，前提是假定您最初认为自己几乎毫无实力。

相比之下，如果您发现自己的让分盘胜率不足 54%，但仍可盈利，那么要想真正认清自身实力，需要的时间将更长。如果关于某人能否成为高水平博彩玩家的初始先验置信度为概率 1%，那么经过 1000 次投注后，此值也不过是上升到 20%。

最后一个图反映了在同等条件（1000 次投注历史和 10 个假设胜率）下得到的一组类似的理想化预期 p 值。我们可通过一个等式来针对投注次数、投资回报率和投注赔率的任意组合近似计算“t 分数”，因此不需要进行蒙特卡罗模拟。同样，曲线颜色越深，表示假设胜率越大（从 51% 到 60%）。

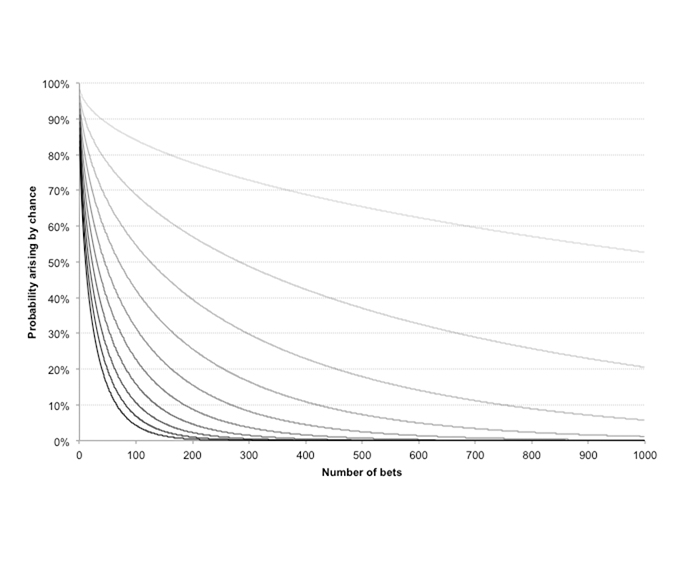
假设胜率为 57%，则经过 200 次投注后，统计显著性 p 值即会小于 5%，而经过约 335 次投注后，统计显著性 p 值将小于 1%。然而，要重申一点，这些信息反映的并不是博彩的实力水平，而只是假定无任何实力的条件下此历史的偶发可能性。

此外，与贝叶斯方法中的初始先验概率类似，这些统计显著性水平只是基于主观判断。然而，与贝叶斯模型类似，如果考虑到这些注意事项，p 值统计检验不失为一个好方法，能够让博彩玩家评估自身实现长期盈利预期的实力。

撇开其他作用不谈，贝叶斯和频率派分析能够再次提醒博彩玩家，在博彩中稳定获利需要从长计议。千万不要以为几场胜利就足以作为判断自身实力的依据。