经典抛硬币示例
二项标准差
大数法则是敌是友?

博彩往往会受到运气的影响。有时候,好运气会让我们大赚一笔,但有时候,坏运气却会让我们损失惨重。理解运气在博彩中的角色至关重要,不过好运气和坏运气的界限到底有多模糊?继续阅读,找出答案。
体育博彩基本上就是在和机会打交道。那些盈利的人几乎全是靠好运气;博彩公司的抽水和大数法则终将摧毁他们。过去几年来经常阅读我文章的人都知道,当谈论博彩玩家长期盈利的实际可能性时,我从不粉饰我对此的消极看法。我并不期待你的同意,因为这就是所有博彩玩家在希望和现实之间斗争的战场。
与此背道而驰地,平博博彩资源板块中的众多文章都意在教博彩玩家更熟练地预测比赛结果。无论如何,哪怕那些确实成功找到有利可图的长期预期价值的人也会遭遇概率法则。在这篇文章中,我将深入探讨概率法则如何发生作用。我将特别说明好运气和坏运气之间的界限到底有多模糊。
经典抛硬币示例
我们都知道抛硬币是个50-50的二元命题:非正面即反面。我们还知道如果抛20次硬币,我们不会一直得到10次正面和10次反面,尽管这是最可能的结果。有时候我们得到12次正面和8次反面,有时候正好相反。得到5次正面和15次反面的情况非常少见。我们可以使用二项分布来确定每种可能结果的准确概率。抛20次硬币的情况如下。
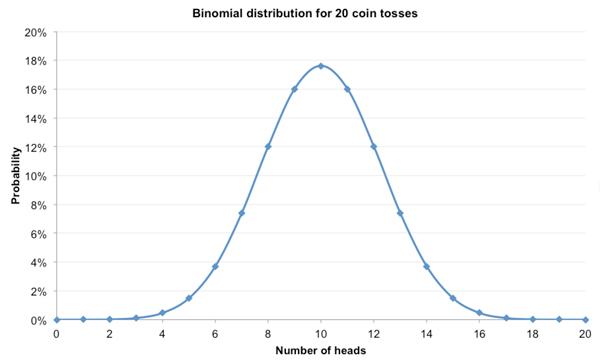
大多数可能的结果值域在5次正面和15次反面到15次正面和5次反面之间。那抛100次硬币呢?二项分布如下所示。
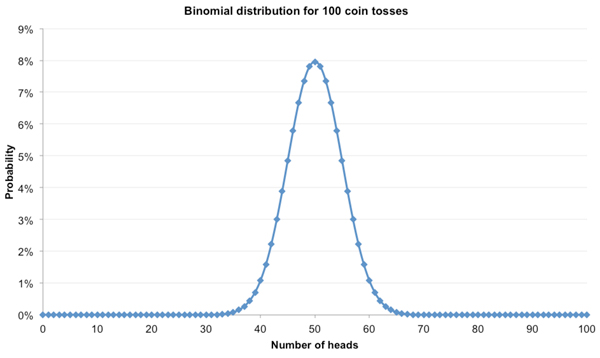
这一次,可能结果的值域更大。由图可知,抛20次硬币的结果值域在5次正面到15次正面之间,差异为10。如果抛100次硬币,那么结果值域在40次正面到60次正面之间,差异基本上翻了一倍。这是否意味着抛硬币样本大小越大,可能结果的值域也越大?嗯,这不一定。
数学家雅各布·伯努利在对这种情况进行实验时,观察到虽然随着样本大小的增加,正面和反面数量之间的绝对数值差可能变大,但是得到正面结果的百分比却越来越接近50%。抛20次硬币得到5次正面的百分比等于5%;而100次中得到40次正面的百分比却等于40%。第二种解释构成了大数法则的基础,是博彩玩家理解概率的重要部分。
二项标准差
我们可以通过标准差来测定分布中显示的值域或离差。对于二项分布,标准差σ由以下简单的等式得出。
![]()
式中,n是二元重复的次数(即抛硬币的次数),p是成功概率(正面),q是失败概率(反面)。由于p + q = 1:
![]()
并且在以下简单的情况中:p = q (0.5):
![]()
如果抛20次硬币,那么σ = 2.24,如果抛100次硬币,那么σ = 5。
从标准差中可知大部分可能结果的值域。例如,如果抛100次硬币,那么略高于三分之二的样本结果将在±1σ之间,或者说在45次到55次正面之间。
我们确认了伯努利的第一个发现:样本大小越大,绝对差额就越大。不过,如果我们不用绝对数字,而使用正面结果百分比的话,情况又如何呢?为了计算出正面结果的百分比,我们将它们的数量除以抛硬币的总次数n。同样地,为了计算出标准差的百分比,我们也必须将其除以n。
因此,对于简单的50:50二元命题:
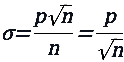
现在,抛20次硬币时正面结果百分比的标准差为0.11(11%),但是抛100次硬币时仅为0.05(5%)。
大数法则
根据大数法则,实验次数越多,得出的平均结果就应该越接近预期价值。对抛硬币而言,我们抛的次数越多,正面结果的百分比就应该越接近50%的预期价值。
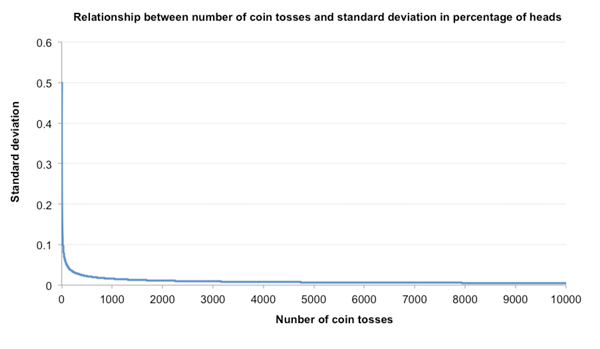
由于标准差百分比和抛硬币次数的平方根成正比,因此这两个变量形成了所谓的幂律关系,其中标准差随着抛掷次数的幂或对数而变化。在双对数坐标系上,两者的关系为一条直线;对应n的每个平方,σ值减半。
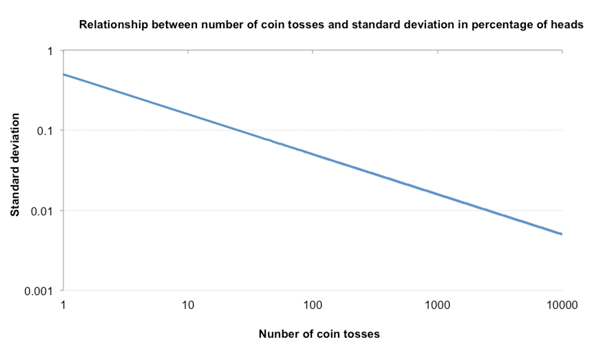
这个幂律关系意味着,在比例上看,标准差的下降大部分发生在最初几次实验中。抛1次硬币之后σ=0.5,等到才抛了25次之后就降到了仅0.1,降幅为(抛掷无数次之后的)极限值零的五分之四。通过这种方式,大数法则实际发生作用的速度之快可见一斑。使用线性比例重绘上表,应该能更直观地看出这一速度。
博彩中的输赢
博彩中的输赢就好比抛硬币中的正反面。投注本质上就是个二元命题:非赢即输。因此,对于那种每次获胜的预期概率都相同的最简单的投注历史,可能的结果也会呈现二项分布。
这个二元命题的一个很明显的例子就是美国体育市场中的分差投注或橄榄球亚洲让分盘,其中一方或另一方的让分使这个投注变成了50-50的二元命题,公平赔率为2.00。
然而,我们不需要将自己限制于50-50的二元命题。回想一下上文关于标准差百分比的等式。下面是更为通用的版本,可以考虑其他可能的预期赢率。
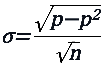
即使对于有能力获得长期盈利预期价值的娴熟博彩玩家,大多数情况也不过是围绕着相对较弱的信号的随机噪音,这是因为类似体育赛事这样的复杂系统固有的随机变异性。
当然在现实中的博彩世界里,没有技巧的博彩玩家只靠满足预期无法实现收支平衡。将博彩公司的抽水纳入考量范围之后,基本上就无法避免在1,000个投注之后输钱了。
设想某位博彩玩家进行50-50的二元投注,长期赢率为55%。通过自己的预测技术,他们将自身的预期赢率从50%提高到了55%,但是同样的二项方差规则仍旧适用。
通过上文中的等式可知,他们在275个投注后的赢率标准差应为3%,这意味着在这个数量的投注历史中,他们的赢率在52%至58%之间的可能性大约为三分之二。
如果我们的投注历史仍旧很简单,每个投注的预期赢率(赔率)相同,那么我们可以使用二项分布来大致判断出现任何情况的概率(在Excel中可以使用函数BINOMDIST来确定)。
我已经用下面这一系列投注历史说明了这一点。第一个是只有20个投注组成的投注历史。图中的数值显示实际赢率的累积概率高于特定值。例如,如果你的长期预期为20%,那么赢得超过六个投注(30%)的几率大约为9%。如果你的典型预期是在20个投注中赢得16个,那么你20个全赢的几率大约为1%。
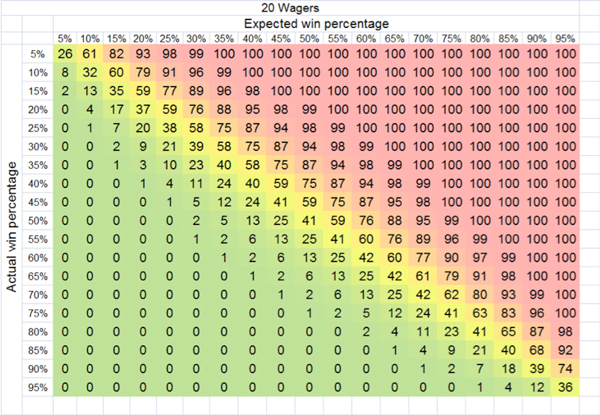
笼统地说,红色和绿色区域分别是公平赔率下的损失区域和盈利区域。毫不奇怪,如果你输掉的投注数量高于预期,就会遭受经济损失,但是你会发现远远低于预期的表现其实并不太常见。
即使在仅仅20个等额赔付投注之后,预期赢得九个甚至更多投注的可能性都达到了四分之三。大数法则站在你这边,保护你免遭可能的巨大百分比损失。
- 阅读:案例研究:为何不允许博彩玩家赢钱?
然而,引申出的推论同样正确。如果你赢得的投注数量高于预期,那么你将会盈利,但是不太可能大赚一笔。即使你是技巧高超的博彩玩家,能将等额赔付投注的长期赢率保持在55%,你从20个投注中赢得14个或更多的几率仍旧只有13%。现在大数法则是你的敌人,让你无法获得较高的百分比收益。
黄色区域是博彩玩家能够实现收支平衡的大致区域。令人惊讶的是,超级好运和超级坏运之间的区域那么小,而大多数投注表现正落在这个区域。
我们再来看看100个投注之后黄色区域会发生什么变化。
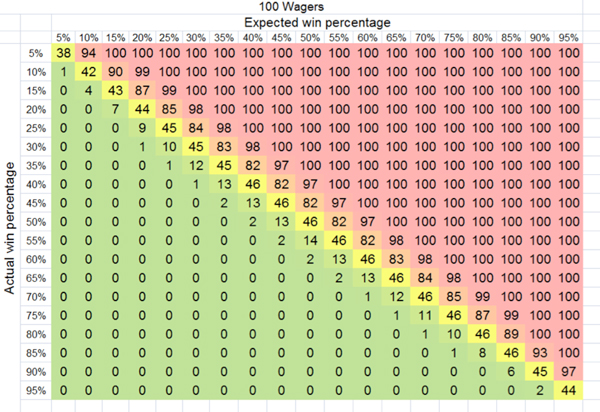
你发现自己远低于长期预期的几率大大缩小。那么1,000个投注之后呢?
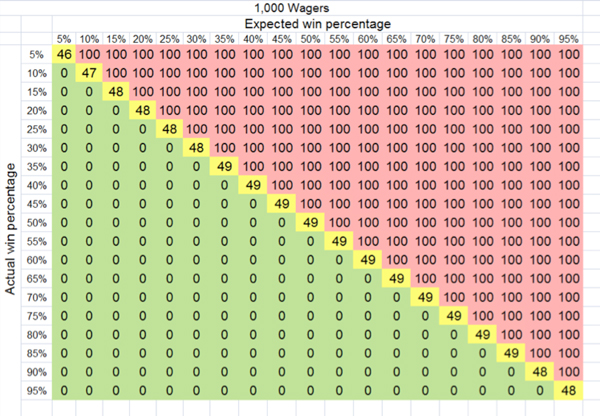
当然在现实中的博彩世界里,没有技巧的博彩玩家只靠满足预期无法实现收支平衡。将博彩公司的抽水纳入考量范围之后,基本上就无法避免在1,000个投注之后输钱了。大数法则彻底摧毁了你。然而,如果你是技巧纯熟的博彩玩家,情况就截然不同了。
如果你预期赢得1,000个等额赔付投注中的55%,那么你几乎总能至少赢得其中的50%。如果博彩公司的抽水小于他们心目中的和你预期的赢率之间的差异,那么你实现长期盈利的几率将非常可观。备受推崇的网站ProfessionalGambler.com特别强调了这一点:
“成功的体育博彩玩家和长期输钱的博彩玩家的投注赢率之间的差异相对很小。”
现在你应该知道这个差异到底有多小了。对于博彩玩家而言,大数法则既是福又是祸。
显然大部分人的投注不像本文中提到的那么简单,博彩玩家会选择各种各样的赔率和投注本金。要分析它们,就得用更为复杂艰深的数学运算或借助我们的好朋友蒙特卡罗模拟,而这将变得过于复杂。
此外,我没有考虑实际利润和损失的方差,这是另一个有意思的话题,我在之前的文章(赔率越高,利润和损失的方差越大)中略有涉及。
尽管如此,本文的目的是说明大数法则的速度和力量,以及预期和实际结果以及好运气和坏运气之间的一线之差。
检验博彩历史的可信度
在本文结束之前,我还想告诉你如何使用实际赢率的标准差信息来检验情报咨询服务商为了卖给你他们挑选的投注而宣称自己取得的博彩历史成绩的可信度。
以一家让分博彩公司为例,这家公司针对他们的“让分原则”实行“诚实坦率的方法”。这家公司显然知道体育博彩中存在着随机性,他们向客户解释不存在所谓一定会赢的事情,而且“每场比赛中总有运气的成分”。尽管如此,鉴于他们发布的超过11,000个所选投注的赢率为76%,显然,他们已经成功驯服了“它变化无常的个性”。
根据大数法则,实验次数越多,得出的平均结果就应该越接近预期价值。
事实上,仔细研究他们迄今公布的结果,会发现10,312个所选投注的实际赢率为75%(显然缺少一些情报)。尽管其中有一些低价和高价特别投注,94%的赔率都在1.67到2.50之间(或者说隐含赢率在60%到40%之间)。整个样本的平均隐含赢率为52.2%,从中减掉博彩公司的抽水之后,基本上就与50-50的二元命题无异了。
将结果分割为56个月度样本(2014年3月到2018年10月)可知,平均每月所选投注总数为184个,而超过一半的在140个到224个之间。如果我们假设长期预期赢率为75%,那么他们的每月赢率变化率有多大?使用上文等式来计算含有184个所选投注的样本赢率预期标准差,得出的结果为略高于3%。略高于三分之二的样本应该在大约72%至78%之间,而95%的样本应该在大约69%至81%之间。
事实上,每月赢率的标准差是8.6%,远远高于应有的水平。不到40%的价值在75%的±1σ之间,而略高于一半的在±2σ之间。变动幅度实在太大。即使我们假设每月只挑选32个投注(投注数量最少的月份),预期标准差仍旧只有7.7%。
- 什么是回撤?如何管理回撤?
每月赢率标准差为8.6%的情况通常发生在大约25个所选投注的样本上,而不是184个。2014年12月挑选了151个投注,平均隐含赢率预期为51.4%。46.4%的预期赢率出现的概率为一万亿年一次。2015年10月挑选了168个投注(平均隐含赢率预期为48.5%),其中154个(即91.7%)获胜。技术如此高超的情报商有如此优秀的表现大约一百万年才会发生一次。
读者可以自由发挥从这些发现中得出结论。也许你可以说技能水平在短时间内可能会剧烈波动。也许这也暗示了另外一些事情。鉴于之前我已经谈过了利润预期的限制,不过我相信,你早就知道76%的让分盘赢率简直令人失笑,你也不会相信这个“奇迹”。

 千博资讯
千博资讯











 据悉,从5月3日起,邱黛国务秘书的遗体被安置在位于金边市堆谷区234号路的家举行葬礼。5月6日将进行土葬。
据悉,从5月3日起,邱黛国务秘书的遗体被安置在位于金边市堆谷区234号路的家举行葬礼。5月6日将进行土葬。

 据柬媒消息,4月8日上午,国家代元首、柬埔寨人民党主席、国王最高顾问委员会主席洪森亲王接见缅甸驻柬大使Kyaw Soe Min。
据柬媒消息,4月8日上午,国家代元首、柬埔寨人民党主席、国王最高顾问委员会主席洪森亲王接见缅甸驻柬大使Kyaw Soe Min。
 据柬媒消息,3月29日,西港云朗基地海军发布消息,3月31日,西港唐岛南部将举行海军实弹演习,请渔民、游客注意,不要在当天经过上述地区,以免发生意外。
据介绍,演习从当天中午12点至下午3点进行,海军将动用3艘军舰和150人,采用14.5毫米机枪发射实弹,另一艘军舰负责清理演习现场。
据柬媒消息,3月29日,西港云朗基地海军发布消息,3月31日,西港唐岛南部将举行海军实弹演习,请渔民、游客注意,不要在当天经过上述地区,以免发生意外。
据介绍,演习从当天中午12点至下午3点进行,海军将动用3艘军舰和150人,采用14.5毫米机枪发射实弹,另一艘军舰负责清理演习现场。
 3月27日公布的一个民意调查结果,约四分之三菲律宾人反对修宪。
在3月初对1200名成年人的民调中,74%说宪法不应在现在或任何其他时间修改。
记者称:“这一意见,在各个地区和各经济阶层都得到大多数人的赞同(分别从69%至82%,和从58%至80%)。”
反对修宪的比例在2024年3月比去年3月大幅上升了43%。
另一方面,在此次最新的调查中,只有8%的受访者说1987宪法现在就应该修改。另有6%受访者反对现在修宪,但支持由现政府在晚些时候修改。
其余的4%受访者对该事项没有特定意见。
3月27日公布的一个民意调查结果,约四分之三菲律宾人反对修宪。
在3月初对1200名成年人的民调中,74%说宪法不应在现在或任何其他时间修改。
记者称:“这一意见,在各个地区和各经济阶层都得到大多数人的赞同(分别从69%至82%,和从58%至80%)。”
反对修宪的比例在2024年3月比去年3月大幅上升了43%。
另一方面,在此次最新的调查中,只有8%的受访者说1987宪法现在就应该修改。另有6%受访者反对现在修宪,但支持由现政府在晚些时候修改。
其余的4%受访者对该事项没有特定意见。















评论 抢沙发